Short Answer TypeSolve the following initial value problem:
(1 + x y) y dx + (1 – x y) x dy = 0, y (1) = 1.
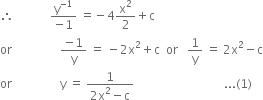
Solve the differential equation;
x (1 + y2 ) dx – y (1 + x2 ) dy = 0 given that y = 0 when x = 1.
Long Answer TypeShort Answer Type
given that y = 0 when x = 0.
Find the equation of the curve passing through the point (1, 1) whose differential equation is x dy = (2 x2 + 1) dx (x ≠ 0).
Long Answer Type
given that y = 1, when x = 0.
Switch
