 Short Answer Type
Short Answer TypeSolve the following initial value problem:
(1 + x y) y dx + (1 – x y) x dy = 0, y (1) = 1.
The given differential equation is
(1 + e2x ) dy + (1 + y2 ) ex dx = 0 or (1 + e2x ) dy = - (1 + y2 ) ex dx![]()
![]()
Let I = ![]()
Put ![]()
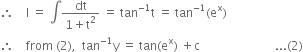
Now, x = 0, y = 1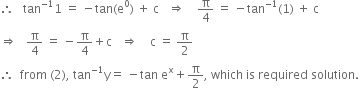
Solve the differential equation;
x (1 + y2 ) dx – y (1 + x2 ) dy = 0 given that y = 0 when x = 1.
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeFind the equation of the curve passing through the point (1, 1) whose differential equation is x dy = (2 x2 + 1) dx (x ≠ 0).
 Long Answer Type
Long Answer Type