 Long Answer Type
Long Answer TypeThe given differential equation is
![]()
Comparing it with ![]()
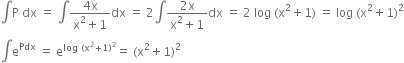
![]() solution of given differential equation is
solution of given differential equation is
![]()
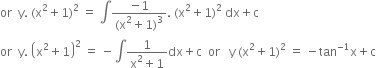
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type