Proof:

                 

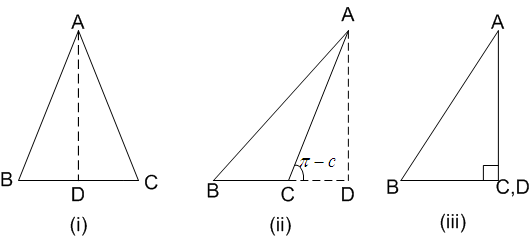
Let angle C be acute in figure (i), obtuse in figure (ii) and the right angle in figure (iii)

In each triangle, draw AD perpendicular on BC i.e.  (on produced if necessary)

In each figure,     

or                            AD = c sinB                                                              ...(i)
                                                                                                  [∵ AB = C]

In figure (i),           

or                           AD = b sinC                                                   [∵ AC = b]

In figure (ii),           

or                             AD = b sinC

In figure (iii),             

or                               AD = b sinC

In all figures,                AD = b sin C                                                         ...(ii)

By (i) and (ii), we get

                  

Similarly,              

Hence,