Proof:

                 

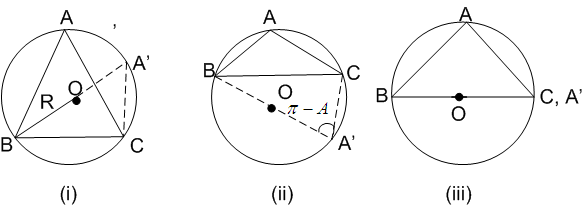
Let  be acute in figure (i), obtuse in figure (ii) and right angle in figure (iii)

Join BO and produce it to meet the circle in A' and join CA',

then triangle BCA' is a right angle triangle in (i) and (ii), but C and A' coincide in (iii).

In figure (i),

Since angles in the same segment are equal 

∴          
                                                           [By sine formula]

                                                                    [∵ BCA' = ]

In figure (ii),  

                 

                                     (∵ Sum of opposite angles of a cyclic quadrilateral is )
i.e.                      

In figure (iii),      

                                                     [∵  i.e. angle is semi-circle]
In all cases, we have

                      

But,             

Hence,