Let angle C be acute in figure (i), obtuse in figure (ii) and right angle in figure

(on produced if necessary)

(iii) Draw AD ⊥ BC in all the triangles.

           

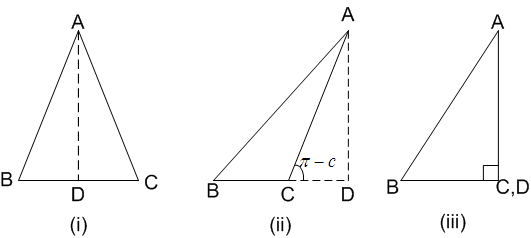
In figure (i),          

                                 = c cos B + b cos C                                                             ...(i)

In figure (ii),              
                                  = c cos B + b cos C                                                             ...(ii)

In figure (iii),               

                                     = c cos B + b cos C                                                         ...(iii)

From (i), (ii) and (iii), we have
                                     a = b cos C + c cos B
Simillarly, we can prove
                             b = c cos A + a cos C
                             c = a cos B + b cos A