 Multiple Choice Questions
Multiple Choice QuestionsA person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g=9.8 ms−2:
2.45 ×10−3 kg
6.45 x×10−3 kg
9.89 ×10−3 kg
9.89 ×10−3 kg
When a rubber band is strecthed by a distance x, it exerts a restoring force of magnitude F = ax +bx2, where a and b are constants. The work done in stretching are unstretched rubber-band by L is
aL2 +bL2
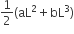
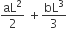
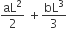
This question has statement 1 and statement 2. Of the four choices given after the statements, choose the one that best describes the two statements.
If two springs S1 and S2 of force constants k1 and k2, respectively, are stretched by the same force, it is found that more work is done on spring S1 than on spring S2.
Statement 1: If stretched by the same amount, work done on S1, will be more than that on S2
Statement 2 : k1 < k2
Statement 1 is false, Statement 2 is true
Statement 1 is true, Statement 2 is false
Statement 1 is true, Statement 2 is the correct explanation for statement 1
Statement 1 is true, Statement 2 is the correct explanation for statement 1
Work done in increasing the size of a soap bubble from a radius of 3 cm to 5 cm is nearly. (Surface tension of soap solution = 0.03 Nm-1)
4π mJ
0.2π mJ
2π mJ
2π mJ
An athlete in the Olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
200 J − 500 J
2 × 105J − 3 × 105J
20,000 J − 50,000 J
20,000 J − 50,000 J
A particle of mass 100 g is thrown vertically upwards with a speed of 5 m/s. the work done by the force of gravity during the time the particle goes up is
0.5 J
-0.5 J
−1.25 J
−1.25 J
The potential energy of a 1 kg particle free move along the x-axis is given by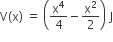
The total mechanical energy of the particle 2 J. Then, the maximum speed (in m/s) is
2
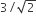


A spherical ball of mass 20 kg is stationary at the top of a hill of height 100 m. It rolls down a smooth surface to the ground, then climbs up another hill of height 30 m and finally rolls down to a horizontal base at a height of 20 m above the ground. The velocity attained by the ball is
40 m/s
20 m/s
10 m/s
10 m/s
A uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
7.2 J
3.6 J
120 J
120 J
A force  is applied over a particle which displaces it from its origin to the
is applied over a particle which displaces it from its origin to the 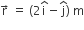 .The work done on the particle in joules is
.The work done on the particle in joules is
-7
+7
+10
+10
