CBSE
 Multiple Choice Questions
Multiple Choice Questions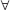 n ∈ N
n ∈ N
r !
n!
n+r+1
(n+r)!
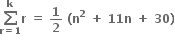 તો k =- ....... .
તો k =- ....... .
n + 6
n + 7
n + 5
n + 4
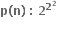 નો એકમનો અંક ....... છે. n > 1
નો એકમનો અંક ....... છે. n > 1
0
4
6
2
1
4
2
5
n = 4 માટે સત્ય નથી.
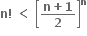 નું પાલન થાય તેવો નાનામાં નાનો ધનપૂર્ણાંક ........ છે. જ્યાં [] મહત્તમ પૂર્ણાંક વિધેય છે.
નું પાલન થાય તેવો નાનામાં નાનો ધનપૂર્ણાંક ........ છે. જ્યાં [] મહત્તમ પૂર્ણાંક વિધેય છે.
6
3
4
2
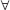 n ∈ N .......... ના ગુણકમાં છે.
n ∈ N .......... ના ગુણકમાં છે.
4
7
5
2
1275
1225
2450
1375
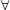 n ∈ N
n ∈ N
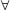 n ∈ N, n > 1
n ∈ N, n > 1
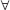 n ∈ N, n ≥ 3
n ∈ N, n ≥ 3
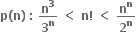 દરેક n ≥ k, n ∈ N માટે સત્ય છે, તો k = .......... .
દરેક n ≥ k, n ∈ N માટે સત્ય છે, તો k = .......... .
6
5
4
3