CBSE Gujarat Board Haryana Board
Class 10 Class 12
ધારો, કે ટાવરનું પ્રતિનિધિત્વ કરે છે. તેના પાયાથી 100 મીટર દૂર બિંદુ O છે. OB એ બિંદુ Oનું ટાવરથી અંતર છે અને AOB ઉત્સેધકોણ છે, તો
OB = 100 મી અને mBOA = 60
AOBમાંં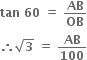
AB = 100 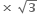
AB = 100 1.73
=173