 Multiple Choice Questions
Multiple Choice QuestionsThe electric field in a certain region is acting radially outward and is given by E = Ar. A charge contained in a sphere of radius 'a' centred at the origin of the field will be given by




In a coil of resistance 10Ω, the induced current developed by changing magnetic flux through it is shown in the figure as a function of time. The magnitude of change in flux through the coil in weber is 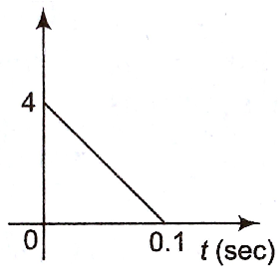
8
2
6
6
What is the flux through a cube of side a if a point charge of q is a one of its corner?
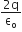
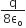
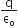
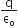
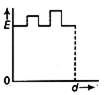
Two thin dielectric slabs of dielectric constants K1 and K2 (K1 < K2) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by: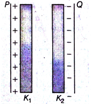


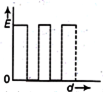
A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the centre of the sphere respectively are:
zero and ![]()
![]()
![]()
![]()
In a region, the potential is represented by V (x,y,z) = 6x - 8 xy - 8y + 6yz, where V is in volts and x, y, z are in metres. The electric force experienced by a charge of 2 coulomb situated at point (1,1,1) is,
6√5 N
30 N
24 N
24 N
A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will
be reduced to half
remain the same
be doubled
be doubled
A beam of cathode rays is subjected to crossed Electric (E) and magnetic field (B). The fields are adjusted such that the beam is not deflected. The specific charge of the cathode rays is given by
(Where V is the potential difference between cathode and anode)
B2/2VE2
2VB2/E2
2VE2/B2
2VE2/B2
The square surface of side L metre in the plane of the paper is placed in a uniform electric field E (volt/m) acting along the same place at angle θ with the horizontal side of the square as shown in the figure. The electric flux linked to the surface in unit of V-m is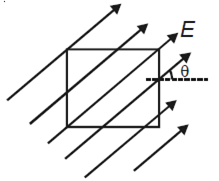
EL2
EL2 cos θ
EL2 sin θ
EL2 sin θ
The electric field at a distance 3R/2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
zero
E
E/2
E/2
