 Multiple Choice Questions
Multiple Choice QuestionsIf the electric fluxes entering and leaving an enclosed surface respectively are Φ1 and Φ2, the electric charge inside the surface will be
(Φ2 − Φ1) ε0
(Φ1 + Φ2) / ε0
(Φ2 − Φ1) / ε0
(Φ1 + Φ2) / ε0
Shown below is a distribution of charges. The flux of electric field due to these charges through the surface is
zero
Two point charges + q and + 4q are located at x = O and x = L respectively. The location of a point on the x-axis at which the net electric field due to these two points charges is zero, is
L / 3
2 L
4 L
8 L
If electric flux entering and leaving an enclosed surface is and respectively, the electric charge inside the enclosed surface will be
The electric field in a region is given by E = V/m. The net flux passing through a square area of side 4 m parallel to y-z plane is
32 V-m
16 V-m
12 V-m
64 V-m
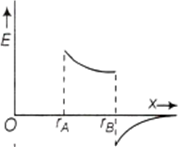
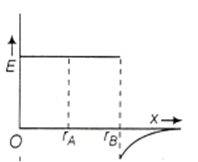
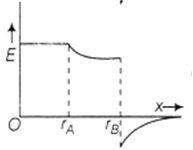
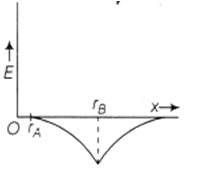
Two concentric conducting spherical shells A and B having radii rA and rB (rB > rA) are charged to QA and -QB . The electric field along a line passing through the centre is
Two charged spheres separated by a distance d exert some force (F) on each other. If they are immersed in a liquid of dielectric constant 4, then what is the force exerted, if all other conditions are same ?
2F
4F
A charge q is located at the centre of a cube. The electric flux through any face is
A.
According to Gauss's theorem, electric flux through the cube (closed surface),
Since, cube has six surfaces and all the faces are symmetrical, therefore electric flux through any face
An electron enters uniform electric field maintained by parallel plates and of value E Vm-1 with a velocity v ms-1 , the plates are separated by a distance d metre, then acceleration of the electron in the field is
The electrostatic field due to a charged conductor just outside the conductor is
zero and parallel to the surface at every point inside the conductor
zero and is normal to the surface at every point inside the conductor
parallel to the surface at every point and zero inside the conductor
normal to the surface at every point and zero inside the conductor
