 Long Answer Type
Long Answer Type(a) Define electric dipole moment. Is it a scalar or a vector? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.
Electric dipole moment is the product of either charges or the distance between two equal and opposite charges.
It is a vector quantity.
Electric dipole moment at a point on the equatorial plane:
Consider a point P on broad side on the position of dipole formed of charges + q and - q at separation 2l. The distance of point P from mid-point O of electric dipole is r. 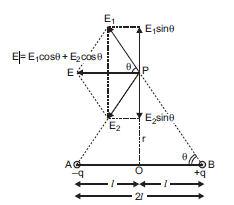
Let E1 and E2 be the electric field strength due to charges +q and –q of electric dipole.
From the fig. we have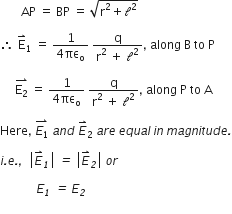
Now, in order to find the resultant electric field, we resolve the components along and perpendicular to AB.
The components perpendicular to AB are sin components and they being equal and opposite to each other cancel each other.
Therefore,
Resultant electric field is given by,
E1 = E1cos θ + E2 cos θ
But, ![]()
From the fig. we can see that,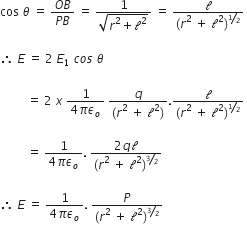
If dipole is infinitesimal and point P is far away, then l2 can be neglected as compared to r2.
Therefore, ![]()
b) Equipotential surfaces due to an electric dipole is given by,
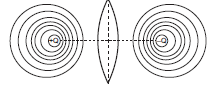
Electric potential is zero at all points in the plane passing through the dipole equator.
Using Gauss’ laws deduce the expression for the electric field due to a uniformly charged spherical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r > R and r < R. (r being the distance from the centre of the shell).
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number ni ) to the lower state, (nf ).
When electron in hydrogen atom jumps from energy state ni =4 to nf =3, 2, 1, identify the spectral series to which the emission lines belong.
(a) Draw the plot of binding energy per nucleon (BE/A) as a function of mass number A. Write two important conclusions that can be drawn regarding the nature of nuclear force.
(b) Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
(c) Write the basic nuclear process of neutron undergoing –decay. Why is the detection of neutrinos found very difficult?
