If g is the acceleration due to gravity on the earth’s surface, the gain in the potential energy of object of mass m raised from the surface of the earth to a height equal to the radius R of the earth is
2 mgR
mgR/2
mgR/4
mgR/4
B.
mgR/2
Gravitational potential energy of body on earth's surface
At a height h from earth's surface, its value is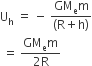
where Me = mass of earth
m = mass of body
R = radius of earth
A satellite of mass m revolves around the earth of radius R at a height x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
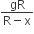
gx
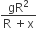
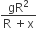
D.
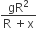
The gravitational force exerted on satellite at a height x is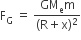
where Me = mass of earth Since, gravitational force provides the necessary centripetal force, so,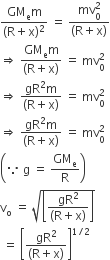
A particle of mass 10 g is kept on the surface of a uniform sphere of mass 100 kg and radius 10 cm. Find the work to be done against the gravitational force between
(you may take G = 6 . 67× 10-11 Nm2/ kg2)
13.34 x 10-10 J
3.33 x 10-10 J
6.67 x10-9 J
6.67 x10-9 J
D.
6.67 x10-9 J
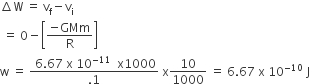
The time period of an earth satellite in circular orbit is independent of
the mass of the satellite
radius of its orbit
both the mass and radius of the orbit
both the mass and radius of the orbit
A.
the mass of the satellite
Time period of satellite
where R + h = orbital radius of satellite,
Me = mass of earth Thus, time period does not depend on the mass of the satellite.
A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same which one of the following will not be affected?
moment of inertia
angular momentum
angular velocity
angular velocity
B.
angular momentum
In free space, neither acceleration due to gravity for external torque act on the rotating solid sphere. Therefore, taking the same mass of sphere if the radius is increased then a moment of inertia, rotational kinetic energy and angular velocity will change but according to the law of conservation of momentum, angular momentum will not change.
