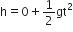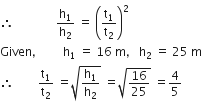Two satellites of earth S1 and S2, are moving in the same orbit. The mass of S1 is four times the mass of S2. Which one of the following statement is true?
The time period of S1 is four times that of S2
The potential energies of earth and satellite in the two cases are equal
S1 and S2 are moving with the same speed
S1 and S2 are moving with the same speed
C.
S1 and S2 are moving with the same speed
In same orbit, orbtial speed of satellites remains same. When two satellites of earth are moving in same orbit, then time period of both are equal.
From Kepler's third law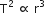
Time period is independent of mass, hence their time periods will be equal.
The potential energy and kinetic energy are mass dependent, hence the PE and KE of satellites are not equal.
But, if they are orbiting in a same orbit, then they have equal orbital speed.
Suppose the charge of a proton and an electron differ slightly. One of them is –e, the other is (e + Δe). If the net of electrostatic force and gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart is zero, then Δe is of the order of [Given mass of hydrogen
mh = 1.67 × 10–27 kg]
10–20 C
10–23 C
10–37 C
10–37 C
C.
10–37 C
Fe = Fg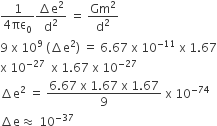
The earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the earth. The escape velocity of a body from this platform is fve, where ve is its escape velocity from the surface of the earth. The value of f is
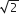

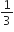
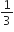
B.

If energy in the form of kinetic energy which is equal to binding energy, is supplied to the sphere, it leaves the gravitational field of earth.
At a platform at a height h,
escape energy = binding energy of sphere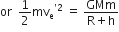
or 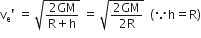
But at surface of earth,
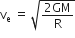
As given, 
Hence, 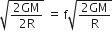
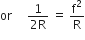
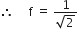
Two bodies, A (of mass 1 kg) and B (of mass 3 kg) are dropped from heights of 16 m and 25 m, respectively. The ratio of the time taken by them to reach the ground is
5/4
12/5
5/12
5/12
D.
5/12
As bodies are dropped from a certain height, their initial velocities are zero i.e., u = 0.
For free fall from a height u = 0 (initial velocity).
From second equation of motion
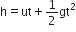
or