Let us consider a liquid of density ρ in a vessel as shown in figure. Let us find the pressure difference between two points A and B separated by vertical height h.
To evaluate the pressure difference between A and B, consider an imaginary cubiod of area of cross-section a of liquid with upper and lower cap passing through A and B respectively. The volume of the imaginary cylinder is,.
V=ah
Mass of liquid of imaginary cylinder is,
m = ρah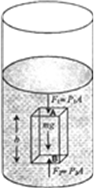
Let P1 and P2 be the pressure on the upper and lower face of cylinder. The different forces acting on the imaginary cylinder are:
(i) weight mg = ρahg in vertically downward direction.
(ii) Downward thrust of F1 =P1a on upper cap.
(iii) Upward thrust of F2 = P2a on lower face. As the imaginary cylinder in the liquid is in equilibrium, therefore the net force on the cylinder is zero, i.e.
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/PHEN11039275-1.png)
Thus the pressure difference between two points separated vertically by height h in the presence of gravity is ρgh. In the absence of gravity this pressure difference becomes zero.
Hydraulic lift is a machine used to multiply the force and it is based on Pascal law.
Hydraulic lift consists of two cylinders of different cross-sectional areas connected with a pipe. The cylinders are filled with incompressible liquid and frictionless pistons are fitted in both the cylinders as shown in figure.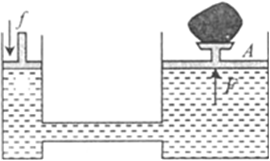
Let a and A be the area of cross-section of smaller piston and bigger piston respectively. The load to be lifted is placed on bigger cross-section and effort is applied on smaller piston. Let a force f be applied on the smaller piston. The pressure exerted by f on piston is,![]()
According to Pascal law, the pressure transmitted to bigger piston is also P. Thus force on bigger piston is,![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/PHEN11039274-2.png)
i.e. The transmitted force gets multiplied by factor η of applied force.
State and prove Pascal's law.
If some pressure is applied at any point of incompressible liquid then the same pressure is transmitted to all the points of liquid and on the walls of the container.
Let us imagine an arbitrary right angled prismatic volume in the liquid of density ρ in equilibrium as shown in figure.
The area of faces ABFE, ABDC and CDFE are ad, bd and cd respectively. Let the pressure of liquid on faces ABFE, ABDC and CDFE be P1, P2 and P3 respectively.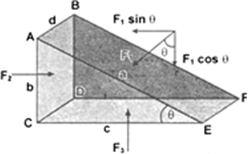
The pressure of liquid exerts the force normal to the surface. Let us assume pressure P1exerts the force F on the surface ABFE, pressure P2 exerts the force F2 on the surface ABDC and pressure P3 exerts force on the surface CDFE.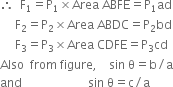
Since the prism is in equilibrium, therefore net force on the prism is zero. Thus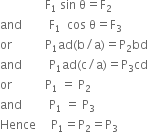
Hence the Pascal's law is proved.
