Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Long Answer Type

201. Show that the following differential equation is homogeneous and find a primitive of it. Derive the solution wherever possible:

1 over straight x cos straight y over straight x dx minus open parentheses straight x over straight y sin straight y over straight x plus cos straight y over straight x close parentheses dy space equals 0

74 Views

202. Show that the following differential equation is homogeneous and find a primitive of it. Derive the solution wherever possible:

2 space straight y space straight e to the power of straight x over 4 end exponent space dx plus open parentheses straight y minus 2 space straight x space straight e to the power of straight x over straight y end exponent close parentheses space dy space equals space 0

73 Views

203. Show that the following differential equation is homogeneous and find a primitive of it. Derive the solution wherever possible:

straight y space dx space plus space straight x space open parentheses log space straight y over straight x close parentheses space dy space minus space 2 space straight x space dy space equals space 0

74 Views

204. Show that the given differential equation is homogeneous and solve it:

left parenthesis straight x squared plus xy right parenthesis space dy space equals space left parenthesis straight x squared plus straight y squared right parenthesis space dx

75 Views

Short Answer Type

205. Show that the given differential equation is homogeneous and solve it:

straight y apostrophe space equals space fraction numerator straight x plus straight y over denominator straight x end fraction

73 Views

206. Show that the given differential equation is homogeneous and solve it:
(x-y) dy - (x+y) dx = 0

74 Views

207. Show that the given differential equation is homogeneous and solve it:
$open parentheses straight x squared minus straight y squared close parentheses space dx space plus space 2 xy space dy space equals space 0$

The given differential equation is
$open parentheses straight x squared minus straight y squared close parentheses dx plus 2 xy space dy space equals space 0 space space or space space space 2 xy space dy space equals space left parenthesis straight y squared minus straight x squared right parenthesis space dx$

or $dy over dx space equals fraction numerator straight y squared minus straight x squared over denominator 2 xy end fraction$
It is a differential equation of the form $dy over dx space equals straight F left parenthesis straight x comma space straight y right parenthesis$
Here, $straight F left parenthesis straight x comma space straight y right parenthesis space equals space fraction numerator straight y squared minus straight x squared over denominator 2 space straight x space straight y end fraction$
Replacing x by $λx$ and y by $λy comma$ we get,
$straight F left parenthesis λx comma space λy right parenthesis space equals space fraction numerator straight lambda squared straight y squared minus straight lambda squared straight x squared over denominator 2 space straight lambda squared space straight x space straight y end fraction space equals space fraction numerator straight lambda squared space left parenthesis straight y squared minus straight x squared right parenthesis over denominator straight lambda squared space left parenthesis 2 xy right parenthesis end fraction space equals space straight lambda degree space space left square bracket straight F left parenthesis straight x comma space straight y right parenthesis right square bracket$
∴ F(x, y) is a homogeneous function of degree zero.
∴ given differential equation is a homogeneous differential equation.
Put y = vx so that $dy over dx equals straight v plus straight x dv over dx$

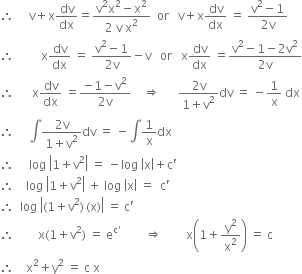
$therefore space space space space space straight v plus straight x dv over dx equals fraction numerator straight v squared straight x squared minus straight x squared over denominator 2 space straight v space straight x squared end fraction space space or space space space straight v plus straight x dv over dx space equals space fraction numerator straight v squared minus 1 over denominator 2 straight v end fraction therefore space space space space space space space space space straight x dv over dx space equals space fraction numerator straight v squared minus 1 over denominator 2 straight v end fraction minus straight v space space space or space space space straight x dv over dx space equals fraction numerator straight v squared minus 1 minus 2 straight v squared over denominator 2 straight v end fraction therefore space space space space space space straight x dv over dx space equals fraction numerator negative 1 minus straight v squared over denominator 2 straight v end fraction space space space space rightwards double arrow space space space space space space fraction numerator 2 straight v over denominator 1 plus straight v squared end fraction dv space equals space minus 1 over straight x space dx therefore space space space space space integral fraction numerator 2 straight v over denominator 1 plus straight v squared end fraction dv space equals space minus integral 1 over straight x dx therefore space space space space space log space open vertical bar 1 plus straight v squared close vertical bar space equals space minus log space open vertical bar straight x close vertical bar plus straight c apostrophe therefore space space space space log space open vertical bar 1 plus straight v squared close vertical bar space plus space log space open vertical bar straight x close vertical bar space equals space space straight c apostrophe therefore space space log space open vertical bar left parenthesis 1 plus straight v squared right parenthesis thin space left parenthesis straight x right parenthesis close vertical bar space equals space straight c apostrophe therefore space space space space space space space space straight x left parenthesis 1 plus straight v squared right parenthesis space equals space straight e to the power of straight c apostrophe end exponent space space space space space space space space rightwards double arrow space space space space space space space space straight x open parentheses 1 plus straight y squared over straight x squared close parentheses space equals space straight c therefore space space space space straight x squared plus straight y squared space equals space straight c space straight x space$
is the required solution.