Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Long Answer Type

231.
Solve the following differential equation:
$dy over dx equals fraction numerator straight x left parenthesis 2 straight y minus straight x right parenthesis over denominator straight x left parenthesis 2 straight y plus straight x right parenthesis end fraction comma space space if space space straight y space equals space 1 space space when space straight x space equals space 1.$

The given differential equation is
$dy over dx equals fraction numerator straight x left parenthesis 2 straight y minus straight x right parenthesis over denominator straight x left parenthesis 2 straight y plus straight x right parenthesis end fraction space space space or space space space dy over dx equals fraction numerator 2 straight y minus straight x over denominator 2 straight y plus straight x end fraction$

Put $straight y space equals space straight v space straight x space space so space that space space dy over dx space equals space straight v plus straight x dv over dx$

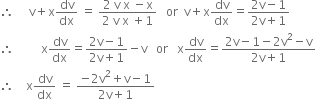
$therefore space space space space space straight v plus straight x dv over dx space equals space fraction numerator 2 space straight v space straight x space minus straight x over denominator 2 space straight v space straight x space plus 1 end fraction space space space or space space straight v plus straight x dv over dx equals fraction numerator 2 straight v minus 1 over denominator 2 straight v plus 1 end fraction therefore space space space space space space space space space straight x dv over dx equals fraction numerator 2 straight v minus 1 over denominator 2 straight v plus 1 end fraction minus straight v space space space or space space space straight x dv over dx equals fraction numerator 2 straight v minus 1 minus 2 straight v squared minus straight v over denominator 2 straight v plus 1 end fraction therefore space space space space straight x dv over dx space equals space fraction numerator negative 2 straight v squared plus straight v minus 1 over denominator 2 straight v plus 1 end fraction$

Separating the variables, we get,

$fraction numerator 2 straight v plus 1 over denominator negative 2 straight v squared plus straight v minus 1 end fraction dv space equals space 1 over straight x dx$

Integrating, $integral fraction numerator 2 straight v plus 1 over denominator negative 2 straight v squared plus straight v minus 1 end fraction dv space equals space 1 over straight x dx$

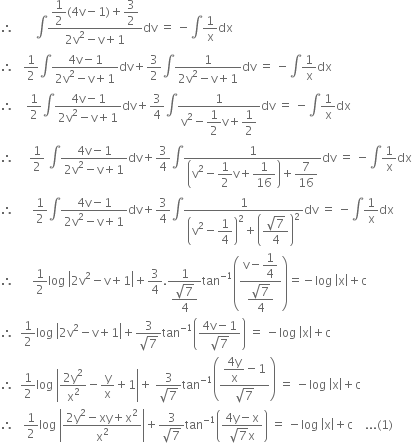
$therefore space space space space space space space integral fraction numerator begin display style 1 half left parenthesis 4 straight v minus 1 right parenthesis plus 3 over 2 end style over denominator 2 straight v squared minus straight v plus 1 end fraction dv space equals space minus integral 1 over straight x dx therefore space space space 1 half integral fraction numerator 4 straight v minus 1 over denominator 2 straight v squared minus straight v plus 1 end fraction dv plus 3 over 2 integral fraction numerator 1 over denominator 2 straight v squared minus straight v plus 1 end fraction dv space equals space minus integral 1 over straight x dx therefore space space space space 1 half integral fraction numerator 4 straight v minus 1 over denominator 2 straight v squared minus straight v plus 1 end fraction dv plus 3 over 4 integral fraction numerator 1 over denominator straight v squared minus begin display style 1 half end style straight v plus begin display style 1 half end style end fraction dv space equals space minus integral 1 over straight x dx therefore space space space space space 1 half space integral fraction numerator 4 straight v minus 1 over denominator 2 straight v squared minus straight v plus 1 end fraction dv plus 3 over 4 integral fraction numerator 1 over denominator open parentheses straight v squared minus begin display style 1 half end style straight v plus begin display style 1 over 16 end style close parentheses plus begin display style 7 over 16 end style end fraction dv space equals space minus integral 1 over straight x dx therefore space space space space space space 1 half integral fraction numerator 4 straight v minus 1 over denominator 2 straight v squared minus straight v plus 1 end fraction dv plus 3 over 4 integral fraction numerator 1 over denominator open parentheses straight v squared minus begin display style 1 fourth end style close parentheses squared plus open parentheses begin display style fraction numerator square root of 7 over denominator 4 end fraction end style close parentheses squared end fraction dv space equals space minus integral 1 over straight x dx therefore space space space space space space 1 half log space open vertical bar 2 straight v squared minus straight v plus 1 close vertical bar plus 3 over 4. fraction numerator 1 over denominator begin display style fraction numerator square root of 7 over denominator 4 end fraction end style end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator straight v minus begin display style 1 fourth end style over denominator begin display style fraction numerator square root of 7 over denominator 4 end fraction end style end fraction close parentheses equals negative log space open vertical bar straight x close vertical bar plus straight c therefore space space 1 half log space open vertical bar 2 straight v squared minus straight v plus 1 close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight v minus 1 over denominator square root of 7 end fraction close parentheses space equals space minus log space open vertical bar straight x close vertical bar plus straight c therefore space space 1 half log space open vertical bar fraction numerator 2 straight y squared over denominator straight x squared end fraction minus straight y over straight x plus 1 close vertical bar plus space fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator begin display style fraction numerator 4 straight y over denominator straight x end fraction minus 1 end style over denominator square root of 7 end fraction close parentheses space equals space minus log space open vertical bar straight x close vertical bar plus straight c space space space therefore space space space 1 half log space open vertical bar fraction numerator 2 straight y squared minus xy plus straight x squared over denominator straight x squared end fraction close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight y minus straight x over denominator square root of 7 straight x end fraction close parentheses space equals space minus log space open vertical bar straight x close vertical bar plus straight c space space space space... left parenthesis 1 right parenthesis$
Now y = 1, when x = 1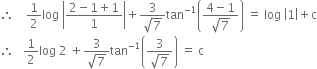
$therefore space space space space 1 half log space open vertical bar fraction numerator 2 minus 1 plus 1 over denominator 1 end fraction close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 minus 1 over denominator square root of 7 end fraction close parentheses space equals space log space open vertical bar 1 close vertical bar plus straight c therefore space space space 1 half log space 2 space plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 3 over denominator square root of 7 end fraction close parentheses space equals space straight c$

Putting this value of c in (1), we get,
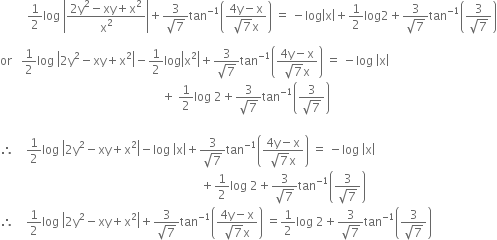
$space space space space space space space space space 1 half log space open vertical bar fraction numerator 2 straight y squared minus xy plus straight x squared over denominator straight x squared end fraction close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight y minus straight x over denominator square root of 7 straight x end fraction close parentheses space equals space minus log open vertical bar straight x close vertical bar plus 1 half log 2 plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 3 over denominator square root of 7 end fraction close parentheses or space space space 1 half log space open vertical bar 2 straight y squared minus xy plus straight x squared close vertical bar minus 1 half log open vertical bar straight x squared close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight y minus straight x over denominator square root of 7 straight x end fraction close parentheses space equals space minus log space open vertical bar straight x close vertical bar space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space plus space 1 half log space 2 plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 3 over denominator square root of 7 end fraction close parentheses space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space therefore space space space space 1 half log space open vertical bar 2 straight y squared minus xy plus straight x squared close vertical bar minus log space open vertical bar straight x close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight y minus straight x over denominator square root of 7 straight x end fraction close parentheses space equals space minus log space open vertical bar straight x close vertical bar space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space plus 1 half log space 2 plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 3 over denominator square root of 7 end fraction close parentheses therefore space space space space 1 half log space open vertical bar 2 straight y squared minus xy plus straight x squared close vertical bar plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 4 straight y minus straight x over denominator square root of 7 straight x end fraction close parentheses space equals 1 half log space 2 plus fraction numerator 3 over denominator square root of 7 end fraction tan to the power of negative 1 end exponent open parentheses fraction numerator 3 over denominator square root of 7 end fraction close parentheses$
which is required solution.

84 Views

232.

Solve the following initial value problem:
$dy over dx space equals space fraction numerator straight y left parenthesis straight x plus 2 straight y right parenthesis over denominator straight x left parenthesis 2 straight x plus straight y right parenthesis end fraction. space space space straight y left parenthesis 1 right parenthesis space equals space 2$

80 Views

Short Answer Type

233. Show that the family of curves for which the slope of the tangent at any point (x, y) on it is

fraction numerator straight x squared plus straight y squared over denominator 2 xy end fraction comma

is given by

straight x squared minus straight y squared space equals space straight c space straight x.

76 Views

Multiple Choice Questions

234. The general solution of the differential equation

fraction numerator straight y space dx space minus space straight x space dy over denominator straight y end fraction space equals space 0

xy = C
x = Cy²
y = Cx
y = Cx

78 Views

235.

A homogeneous differential equation of the from $dx over dy space equals space straight h open parentheses straight x over straight y close parentheses$ can be solved by making the substitution.

y = vx
v = yx
x = vy
x = vy

71 Views

236. Which of the following is a homogeneous differential equation?

(4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(xy) dx – (x³ + y³) dy = 0
(x³ + 2 y²) dx + 2xy dy = 0
(x³ + 2 y²) dx + 2xy dy = 0

82 Views

Short Answer Type

237.

Solve : $dy over dx plus straight y space equals space sin space straight x comma space space left parenthesis straight x space element of space straight R right parenthesis$

73 Views

Long Answer Type

238. Solve the differential equation:

straight x dy over dx minus straight y minus 2 straight x cubed space equals space 0.

74 Views

239. Solve the differential equation:

dy over dx minus 2 straight y space equals space 3 straight x.

80 Views

Short Answer Type

240.

Solve $dy over dx plus straight y over straight x space equals space straight e to the power of straight x comma space space left parenthesis straight x greater than 0 right parenthesis.$