Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Long Answer Type

231.

Solve the following differential equation:
$dy over dx equals fraction numerator straight x left parenthesis 2 straight y minus straight x right parenthesis over denominator straight x left parenthesis 2 straight y plus straight x right parenthesis end fraction comma space space if space space straight y space equals space 1 space space when space straight x space equals space 1.$

84 Views

232.

Solve the following initial value problem:
$dy over dx space equals space fraction numerator straight y left parenthesis straight x plus 2 straight y right parenthesis over denominator straight x left parenthesis 2 straight x plus straight y right parenthesis end fraction. space space space straight y left parenthesis 1 right parenthesis space equals space 2$

80 Views

Short Answer Type

233. Show that the family of curves for which the slope of the tangent at any point (x, y) on it is $fraction numerator straight x squared plus straight y squared over denominator 2 xy end fraction comma$ is given by $straight x squared minus straight y squared space equals space straight c space straight x.$

We know that $dy over dx$ is slope of tangent to the curve at point (x, y).
$therefore space space space space space space space space space dy over dx space equals space fraction numerator straight x squared plus straight y squared over denominator 2 xy end fraction$
Put y = v x so that $dy over dx equals straight v plus straight x dv over dx$
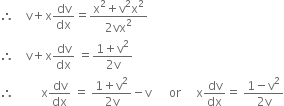
$therefore space space space space straight v plus straight x dv over dx equals fraction numerator straight x squared plus straight v squared straight x squared over denominator 2 vx squared end fraction therefore space space space space straight v plus straight x dv over dx space equals fraction numerator 1 plus straight v squared over denominator 2 straight v end fraction therefore space space space space space space space space space straight x dv over dx space equals space fraction numerator 1 plus straight v squared over denominator 2 straight v end fraction minus straight v space space space space space space or space space space space space straight x dv over dx equals space fraction numerator 1 minus straight v squared over denominator 2 straight v end fraction$
Separating the variables and integrating, we get,
$integral fraction numerator 2 straight v over denominator 1 minus straight v squared end fraction dv space equals space integral 1 over straight x dx space space space space or space space space integral fraction numerator 2 straight v over denominator straight v squared minus 1 end fraction dv space equals space minus integral 1 over straight x dx$

$therefore space space space log space open vertical bar straight v squared minus 1 close vertical bar space equals space minus log space open vertical bar straight x close vertical bar plus log space open vertical bar straight c subscript 1 close vertical bar space space space or space space space log space open vertical bar left parenthesis straight v squared minus 1 right parenthesis thin space left parenthesis straight x right parenthesis close vertical bar space equals space log space open vertical bar straight c subscript 1 close vertical bar or space space space space space space space left parenthesis straight v squared minus 1 right parenthesis space straight x space equals space plus-or-minus space space straight c subscript 1$
Replacing v by $straight y over straight x comma space$ we get

$open parentheses straight y squared over straight x squared minus 1 close parentheses space straight x space equals space plus-or-minus space straight c subscript 1 space space space or space space space space left parenthesis straight y squared minus straight x squared right parenthesis space equals space space plus-or-minus space straight c subscript 1 straight x space space space or space space space straight x squared minus straight y squared space equals space cx.$

76 Views

Multiple Choice Questions

234. The general solution of the differential equation

fraction numerator straight y space dx space minus space straight x space dy over denominator straight y end fraction space equals space 0

xy = C
x = Cy²
y = Cx
y = Cx

78 Views

235.

A homogeneous differential equation of the from $dx over dy space equals space straight h open parentheses straight x over straight y close parentheses$ can be solved by making the substitution.

y = vx
v = yx
x = vy
x = vy

71 Views

236. Which of the following is a homogeneous differential equation?

(4x + 6y + 5) dy – (3y + 2x + 4) dx = 0
(xy) dx – (x³ + y³) dy = 0
(x³ + 2 y²) dx + 2xy dy = 0
(x³ + 2 y²) dx + 2xy dy = 0

82 Views

Short Answer Type

237.

Solve : $dy over dx plus straight y space equals space sin space straight x comma space space left parenthesis straight x space element of space straight R right parenthesis$

73 Views

Long Answer Type

238. Solve the differential equation:

straight x dy over dx minus straight y minus 2 straight x cubed space equals space 0.

74 Views

239. Solve the differential equation:

dy over dx minus 2 straight y space equals space 3 straight x.

80 Views

Short Answer Type

240.

Solve $dy over dx plus straight y over straight x space equals space straight e to the power of straight x comma space space left parenthesis straight x greater than 0 right parenthesis.$