The equation of any plane through (1, 2, 3) is
A(x – 1)+B(y – 2) + C(z – 3) = 0    ...(1)
∵ it passes through (0, – 1, 0)
∴ A (0 – 1) + B (– 1 – 2) + C (0 – 3) = 0
∴  – A – 3B – 3C = 0    ⇒ A + 3B + 3C = 0    ...(2)
Since plane (1) is parallel to the line 
∴  normal to the plane with direction ratios A, B, C is perpendicular to the line with direction ratios 2, 3, – 3.
∴  A(2) + B(3) + C(– 3) = 0    [∵  a₁a₂+ b₁b₂ + c₁c₂ = 0]
∴  2A + 3B-3C = 0
Solving (2) and (3), we get,
           


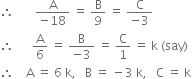
Putting values of A, B, C in (1), we get,
6k(x – 1) + (–3 k)(y – 2) + k(z – 3) = 0 or    6 (x – 1) –3 (y – 2) + (z – 3) = 0
or    6x – 6 – 3y + 6 + z – 3 = 0
or    6x-3y + z=3
which is required equation of plane.