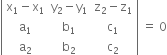Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Long Answer Type

281. Find the vector and cartesian equation of the plane containing the two lines

straight r with rightwards arrow on top space equals space 2 space straight i with hat on top space plus space straight j with hat on top space minus space 3 space straight k with hat on top space plus space straight lambda space left parenthesis straight i with hat on top space plus space 2 space straight j with hat on top space plus space 5 space straight k with hat on top right parenthesis

and

straight r with rightwards arrow on top space equals space 3 space straight i with hat on top space plus space space 3 space straight j with hat on top space minus space 7 space straight k with hat on top space plus space straight mu space left parenthesis 3 straight i with hat on top space minus space 2 space straight j with hat on top space plus space space 5 space straight k with hat on top right parenthesis

72 Views

Short Answer Type

282. Find the equation of the plane containing the lines:

fraction numerator straight x minus 4 over denominator 1 end fraction space equals space fraction numerator straight y minus 3 over denominator 4 end fraction space equals space fraction numerator straight z minus 2 over denominator 5 end fraction

and

fraction numerator straight x minus 3 over denominator 1 end fraction space equals space fraction numerator straight y minus 2 over denominator negative 4 end fraction space equals space straight z over 5

82 Views

Long Answer Type

283. Find the equation of the plane passing through the points (3, 2, 1) and (0, 1, 7) and parallel to the line

straight r with rightwards arrow on top space equals space 2 space straight i with hat on top space minus space straight j with hat on top space plus space straight k with hat on top space plus space straight lambda left parenthesis straight i with hat on top space minus space straight j with hat on top space minus space straight k with hat on top right parenthesis.

74 Views

284. Find the equation of the plane passing through the points (1, 2, 3) and (0. –1, 0) and parallel to the line

fraction numerator straight x minus 1 over denominator 2 end fraction space equals space fraction numerator straight y plus 2 over denominator 3 end fraction space equals space fraction numerator straight z over denominator negative 3 end fraction.

87 Views

285. Find the equation of the plane passing through the points (3, 2, 2) and (1, 0, –1) parallel to the line

fraction numerator straight x minus 1 over denominator 2 end fraction space equals space fraction numerator straight y minus 1 over denominator negative 2 end fraction space equals fraction numerator straight z minus 2 over denominator 3 end fraction.

108 Views

286. Find the equation of the plane passing through the origin and parallel to the vectors

straight i with hat on top space plus space straight j with hat on top space minus space straight k with hat on top space space space and space space 3 space straight i with hat on top space minus space straight k with hat on top.

97 Views

Short Answer Type

287. Find the vector and Cartesian form of the equation of the plane passing through the point (1, 2, –4) and parallel to the lines

straight r with rightwards arrow on top space equals straight i with hat on top space plus space 2 space straight j with hat on top space minus space 4 space straight k with hat on top space plus space straight lambda open parentheses 2 straight i with hat on top space plus space 3 space straight j with hat on top space plus space 6 space straight k with hat on top close parentheses

and

straight r with rightwards arrow on top space equals space straight i with hat on top space minus space 3 space straight j with hat on top space plus space space 5 space straight k with hat on top space plus space straight mu space open parentheses straight i with hat on top space plus space straight j with hat on top space minus space straight k with hat on top close parentheses

87 Views

Long Answer Type

288. Show that the lines:

fraction numerator straight x minus 1 over denominator 2 end fraction space equals fraction numerator straight y minus 2 over denominator 3 end fraction space equals space fraction numerator straight z minus 3 over denominator 4 end fraction space and space fraction numerator straight x minus 4 over denominator 5 end fraction space equals space fraction numerator straight y minus 1 over denominator 2 end fraction space equals straight z

intersect. Find the point of intersection also.

91 Views

289. Show that the lines $fraction numerator straight x plus 3 over denominator negative 3 end fraction space equals space fraction numerator straight y minus 1 over denominator 1 end fraction space equals space fraction numerator straight z minus 5 over denominator 5 end fraction space and space fraction numerator straight x plus 1 over denominator negative 1 end fraction space equals fraction numerator straight y minus 2 over denominator 2 end fraction space equals fraction numerator straight z minus 5 over denominator 5 end fraction$ are coplanar.

The given lines are

fraction numerator straight x plus 3 over denominator negative 3 end fraction space equals fraction numerator straight y minus 1 over denominator 1 end fraction space equals fraction numerator straight z minus 5 over denominator 5 end fraction space and space fraction numerator straight x plus 1 over denominator negative 1 end fraction space equals space fraction numerator straight y minus 2 over denominator 2 end fraction space equals space fraction numerator straight z minus 5 over denominator 5 end fraction

These equations can be written as

fraction numerator straight x minus left parenthesis negative 3 right parenthesis over denominator negative 3 end fraction space space equals fraction numerator straight y minus 1 over denominator 1 end fraction space equals fraction numerator straight z minus 5 over denominator 5 end fraction space and space fraction numerator straight x minus left parenthesis negative 1 right parenthesis over denominator negative 1 end fraction space equals space fraction numerator straight y minus 2 over denominator 2 end fraction space equals space fraction numerator straight z minus 5 over denominator 5 end fraction

∴ x₁ = –3, y₁= 1, z₁ = 5, a₁ = –3, b₁= 1, c₁ = 5
x₂ = –1, y₂ = 2, z₂ = 5, a₂ = –1 b₂ = 2, c₂ = 5
The given lines will be coplanar
if

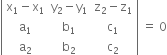
open vertical bar table row cell straight x subscript 1 minus straight x subscript 1 end cell cell straight y subscript 2 minus straight y subscript 1 end cell cell straight z subscript 2 minus straight z subscript 1 end cell row cell straight a subscript 1 end cell cell straight b subscript 1 end cell cell straight c subscript 1 end cell row cell straight a subscript 2 end cell cell straight b subscript 2 end cell cell straight c subscript 2 end cell end table close vertical bar space equals space 0

i.e., if

open vertical bar table row 2 1 0 row cell negative 3 end cell 1 5 row cell negative 1 end cell 2 5 end table close vertical bar space equals space 0

i.e. if

2 space open vertical bar table row 1 5 row 2 5 end table close vertical bar minus 1 open vertical bar table row cell negative 3 end cell 5 row cell negative 1 end cell 5 end table close vertical bar space plus space 0 space open vertical bar table row cell negative 3 end cell 1 row cell negative 1 end cell 2 end table close vertical bar space equals space 0

i.e. if

2 space left parenthesis 5 minus 10 right parenthesis minus 1 space left parenthesis negative 15 plus 5 right parenthesis plus 0 space left parenthesis negative 6 plus 1 right parenthesis space equals space 0

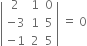
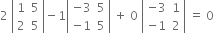
i.e. if –10+10 + 0 = 0
i.e. if 0 = 0, which is true
∴ given lines are coplanar.

82 Views

290. Show that the lines

fraction numerator straight x minus 5 over denominator 4 end fraction space equals space fraction numerator straight y minus 7 over denominator 4 end fraction space equals space fraction numerator straight z plus 3 over denominator negative 5 end fraction

and

fraction numerator straight x minus 8 over denominator 7 end fraction space equals space fraction numerator straight y minus 4 over denominator 1 end fraction space equals space fraction numerator straight z minus 5 over denominator 3 end fraction

intersect each other.

96 Views

Previous Year Papers

Test Series

Test Yourself

Long Answer Type

Short Answer Type

Long Answer Type

Short Answer Type

Long Answer Type

289. Show that the lines are coplanar.