The equation of plane through (3, 2, 2) is
A (x – 3) + B (y – 2) + C (z – 2) = 0    ...(1)
Since it passes through (1, 0, –1)
∴  A (1 – 3) + B (0 – 2) + C (–1 – 2) = 0
or  –2A – 2B – 3C = 0
∴ 2A + 2B + 3C = 0    .,.(2)
The equation of line is
         
Its direction ratios are 2, –2, 3
Since the line is parallel to plane (1) whose normal has direction ratios A, B, C.
∴  normal to plane (1) is perpendicular to line
∴  2A – 2B + 3C = 0    ...(3)
From (2) and (3), we get,
           


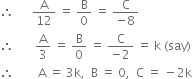
Putting these values of A, B, C in (1), we get,
3k (x – 3) + 0 (y – 2) – 2k (z –2) = 0
or 3 (x – 3) – 2 (z – 2 ) = 0
or 3x – 9 –2z + 4 = 0 or 3x –2z  – 5 = 0