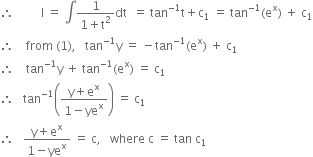Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeFor the following differential equation, find the general solution:
sec2 x tan y dx – sec2 y tan x dy = 0.
 Short Answer Type
Short Answer TypeFor the following differential equation, find the general solution:
sec2 x tan y dx + sec2 y tan x dy = 0.
Solve:
![]()