Solve: from Mathematics Differential Equations

Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Advertisement

Differential Equations

Short Answer Type

141.

Solve:
$open parentheses straight e to the power of straight x plus 1 close parentheses space straight y space dy space plus space left parenthesis straight y plus 1 right parenthesis space straight e to the power of straight x space dx space equals space 0$

87 Views

142.

Solve:
$straight y left parenthesis 1 minus straight x squared right parenthesis space dy space plus space straight x space left parenthesis 1 plus straight y squared right parenthesis space dx space equals space 0.$

83 Views

143.

Solve:
$straight y space logydx space minus space straight x space dy space equals space 0$

91 Views

Long Answer Type

144.

Show that the general solution of the differential equation $dy over dx plus fraction numerator straight y squared plus straight y plus 1 over denominator straight x squared plus straight x plus 1 end fraction space equals 0$ is given by (x + y + 1) = A (1 – x – y – 2 x y), where A is parameter.

77 Views

Advertisement

Short Answer Type

145.

Solve:
$dy over dx space equals space fraction numerator straight x left parenthesis 2 space log space straight x space plus space 1 right parenthesis over denominator sin space straight y space plus space straight y space cosy end fraction$

80 Views

146.

Solve
$dy over dx space equals space fraction numerator xe to the power of straight x logx plus straight e to the power of straight x over denominator straight x space cosy end fraction$

83 Views

Long Answer Type

147.

Solve
$dy over dx space equals space sin cubed straight x space cos squared straight x plus straight x space straight e to the power of straight x$

82 Views

148.

Solve:
$dy over dx space equals space cos cubed straight x space sin to the power of 4 straight x plus straight x square root of 2 straight x plus 1 end root$

84 Views

Advertisement

Advertisement

149.
Solve:
$dy over dx equals negative straight x space sin squared straight x space space equals space fraction numerator 1 over denominator straight x space log space straight x end fraction$

dy over dx minus straight x space sin squared straight x space equals space fraction numerator 1 over denominator straight x space log space straight x end fraction space or space dy over dx space equals straight x space sin squared straight x space plus space fraction numerator 1 over denominator straight x space logx end fraction

Separating the variables, we get,

dy equals open parentheses straight x space sin squared straight x plus fraction numerator 1 over denominator straight x space logx space end fraction close parentheses dx space space space space rightwards double arrow space space integral dy space equals space integral open parentheses xsin squared straight x plus fraction numerator 1 over denominator straight x space logx end fraction close parentheses dx

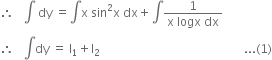
therefore space space space integral space dy space equals integral straight x space sin squared straight x space dx plus integral fraction numerator 1 over denominator straight x space logx space dx end fraction therefore space space space integral dy space equals space straight I subscript 1 plus straight I subscript 2 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis

where

straight I subscript 1 space equals space integral straight x space sin squared space dx space equals space 1 half integral straight x space left parenthesis 2 space sin squared straight x right parenthesis space dx

equals space 1 half integral straight x left parenthesis 1 minus cos space 2 straight x right parenthesis space dx space equals space 1 half integral straight x space dx space minus space 1 half integral straight x. space cos space 2 straight x space dx

equals space straight x squared over 4 minus 1 fourth straight x space sin space 2 straight x space plus space 1 fourth integral sin space 2 straight x space dx space equals space straight x squared over 4 minus 1 fourth straight x space sin 2 straight x space minus 1 over 8 cos space 2 straight x

straight I subscript 2 space equals integral fraction numerator 1 over denominator straight x space logx end fraction dx space equals space integral fraction numerator begin display style 1 over straight x end style over denominator log space straight x end fraction dx space equals space log space open vertical bar log space straight x close vertical bar

therefore space space space from space left parenthesis 1 right parenthesis comma space we space get

,

integral dy space equals space straight x squared over 4 minus 1 fourth straight x space sin space 2 straight x space minus 1 over 8 cos space 2 straight x space plus space log space open vertical bar log space straight x close vertical bar

therefore space space space straight y space equals space straight x squared over 4 minus 1 fourth straight x space sin space 2 straight x space minus space 1 over 8 cos space 2 straight x space plus space log space open vertical bar logx close vertical bar space plus straight c

which is the required solution.

89 Views

Advertisement

150.

Show that the given differential equation is homogeneous and solve it.
(x² – y²) dx + 2xy dy = 0
given that y = 1 when x = 1.

89 Views

Advertisement