Antilogarithms – Definition, Methods, and Examples

You should be familiar with logarithms to understand antilogarithms in a better manner. Logarithms involve determining the power required to raise a given base to obtain a particular number. For example, the logarithm of 10000 with a base 10 is 4, because 10 raised to the power of 4 is equal to 10000.

The Antilogarithms (or Antilog) is the inverse of taking logarithms. The logarithms change numbers into exponents, whereas an antilog performs the inverse operation by converting exponents into numbers. In this article, we will explore the definition of antilog, methods of finding it, and numerous examples with different techniques.

Definition of Antilogarithms

The inverse operation of taking a logarithm is known as antilogarithm. Suppose, x is the logarithm of a number y with base a, then we can say y is the antilogarithm of x to the base a. An Antilog can be defined as, if log _a ^y = x, then, y = antilog _a ^x

The antilogarithm of a number x to the base ‘a’ can be found by raising the base ‘a’ to the power of x. i.e.  y = antilog _a ^x = _a ^x. For example, antilog ₂⁵ = ₂⁵ = 32

Calculation of Antilog

Antilogarithm is determined based on the logarithm numbers. Any logarithmic number has two components: characteristics and mantissa. Characteristic is an integral part that may be positive or negative. Mantissa is a fractional part that is always positive. If the mantissa is negative, it is necessary to convert it to positive. Such as, in the logarithm number 3.3406, 3 is characteristic, and 0.3406 is the mantissa.

Finding Antilog Using Antilog Table To find antilog by using the antilog table, you can follow these steps:

1. Separately write down the mantissa and characteristics of the given logarithmic number.
2. Locate the very left first two digits of the mantissa in the left column and the third digit at the top row of the antilog table. Write the value where both meet inside the antilog table.
3. See the fourth digit of the mantissa at the top row of the means difference, and write the value where the first two digits and fourth digits meet.
4. Add both (step 2 and step 3) obtained values.
5. The characteristic helps us in deciding where the decimal point should be placed.  The decimal point moves to the right from its original place for positive characteristics. While for negative characteristics, the decimal point moves to the left side.

Calculating Antilog without Antilog table

Let’s learn how to determine antilog without an antilog table

1. Find out the base of antilogarithm. The most common base for antilog is 10, but other bases can also be used.
2. Calculate the antilog by raising the base to the exponent of the logarithmic number.
3. The value found in step 2 is an antilog of the logarithm number.

For instance, the antilog of logarithm number 0.5 with a base of 10 is  10^0.5 = 3.1622

Antilog in Calculation.

Log and antilog helps us to simplify the mathematical expressions

• Assign a variable (x, y, or z) to the given expression or number.
• Now, take the logarithm on both sides of the equations.
• Apply the following logarithmic properties to simplify the given expression.

⇒log (A*B) = log A + log B

⇒log (A / B) = log A – log B

⇒log A ⁿ = n log A

• Find the logarithm of each number involved by using a log table or calculator, and simplify the remaining expression.
• Take the antilog on both sides of the equation to get the result of the given expression.

Key Points of Antilog

• The Antilog of 0 is 1.
• Antilogarithms of a negative number are always positive.
• The antilogarithm of a product of two numbers is equal to the addition of the antilogarithms of those two numbers.
• The antilog of a quotient of two numbers is equal to the difference of the antilogarithms of those two numbers.

How to calculate Antilog?

An antilog calculator is a best way to calculate antilog. Here are a few solved examples to learn how to calculate antilog manually.

Example 1:

Determine the antilog of the logarithms number 2.0198 by using the Antilogarithm table.

Solution:

In this example, the Characteristic is 2, and Mantissa is .0198.

Step 1: Locate the very left first 2 digits of the mantissa (.01) in the left column and the third digit (9) at the top row of the antilog table. Write the value where both meet inside the antilog table. Here .01 and 9 meet at 1045.

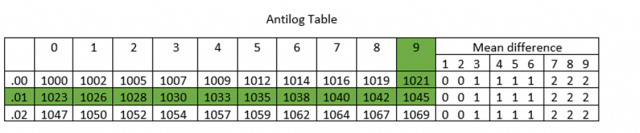
Step 2: Find the fourth digit of the mantissa (8) at the top row of the means difference. Write down the value where the first two digits (.01) and fourth digits (8) intersect. Both intersect at 2.

Step 3: Add found values in steps 2 and 3. (1045 + 2 = 1047)

Step 4: In the case of a characteristic of 2, you would move the decimal point two places to the right from its original position to get the final antilogarithm result.

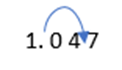
Thus, the antilog of the logarithms number 2.0198 is 104.7

Example 2:

Compute the antilog of logarithms -1.2192 number with a base of 10.

Solution:

Antilog₁₀^-1.2192 =?

Antilog (-1.2192) = 10^-1.2192 = 0.0603

So, the Antilogarithm of -1.2192, with a base of ten is 0.0603

Conclusion

In this article, we talked about antilogarithms in depth. We taught how to evaluate antilog with the help of an antilog table and without using its table. We discussed how log and antilog are used in mathematics to simplify problems. We solved some examples with different methods. After reading this article, you can easily calculate the antilog of any logarithm number.