
Through the standard form offers different advantages in mathematical calculations and scientific notation. Firstly, it allows for easy comparison and estimation of values across different orders of magnitude. Secondly, it simplifies arithmetic operations by reducing the number of significant digits involved.
In this article, we will discuss the basic definition of the standard form of numbers, formula, daily life applications, and solved examples.
What is standard form?
Standard form, also known as scientific notation or exponential notation, is a method of representing very large numbers or very small numbers in a compressed and suitable format. For this reason, this format is particularly useful for handling numbers with many digits/values that vary greatly in magnitude.
In standard form, a number is expressed as the product of a coefficient (a number typically between 1-9) and a power of 10. Therefore, this representation simplifies calculations and comparisons by standardizing the way we express different magnitudes.
Formula:
To illustrate, the below formula is used to represent a standard form of a number:
m × 10n
Where
- “m” is a decimal number greater than or equal to 1 but less than 10
- “n” represents the exponent or power of 10.
Thus, the exponent “n” indicates the number of places the decimal point needs to be shifted to the right or left to obtain the original value.
Working Steps for Expressing a Number in Standard Form
Below are the basic working steps for writing numbers in standard form
1. Identify the Coefficient:
Adjust the decimal point in the original number to obtain a coefficient that is a decimal number greater than or equal to 1 but less than 10.
2. Determine the Exponent:
Count the number of places the decimal point is moved. This count will be the exponent. If the decimal is moved to the left, the exponent is positive; if to the right, the exponent is negative.
3. Write in Standard Form:
Express the number in the form of Coefficient × 10exponent.
These steps provide a clearer and more detailed guide for converting numbers to standard form, which is a useful skill in scientific notation and various mathematical and scientific applications.
Example:
Transform 2,500,000 into standard form.
Solution:
Step 1:
The decimal point in the initial amount should be moved such that it is between 1 and 10.
Step 2:
There was a 6-position move left of the decimal point.
2,500,000 = 2.5 x 10-6.
Step 3:
Hence, 2,500,000 convert into standard form is 2.5 × 10-6.
Implementation operations with numbers in standard form
- Addition/Subtraction: Adjust the exponents to be the same and then operate on the coefficients.
- Multiplication: Reproduce the coefficients together and add the exponents. Once needed, change the outcome so that it is in standard form.
- Partition: Exponents are subtracted after separating the coefficients. When required, change the outcome so that it is in standard form.
Example:
We perform the addition operation below,
(3.4 × 105) + (2.1 × 104).
Solution:
Step 1:
Set the exponents to the exact same value. The following term has to be changed.
(3.4 × 105) + (0.21 × 105)
Step 2:
Perform the addition on the coefficients.
(3.4 + 0.21) × 105 = 3.61 × 105
Step 3:
Therefore, the result of the addition is 3.61 × 105.
Note:
Performing operations with numbers in standard form simplifies calculations and allows for easy manipulation of values across different orders of magnitude.
Examples of writing numbers in standard form.
Here we’ll explore the process of converting numbers into their standard form with the help of solved examples.
Example 1:
Convert 14,000,000 to standard form.
Solution:
Step 1:
Make a starting number between 1 and 10 with a decimal place.
Step 2:
The decimal point was moved 7 places to the left.
14,000,000 = 1.4 x 10-7.
Step 3:
The number 14,000,000 in standard form is 1.4 × 10-7.
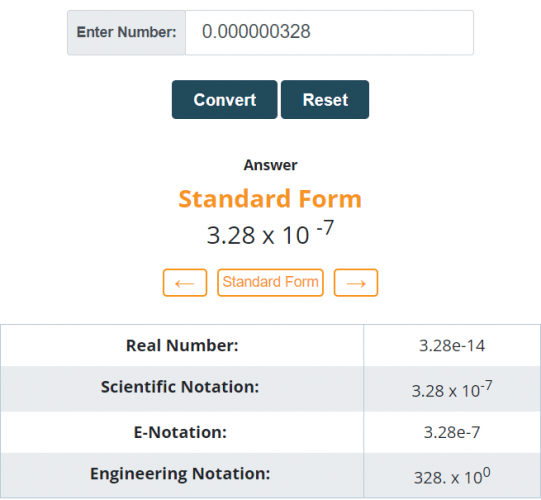
Example 2:
Convert 0.000000328 to standard form.
Solution:
Step 1:
Move the decimal point until it lies between 1 and 10.
Step 2:
The decimal point was moved 7 places to the right.
0.000000328 = 3.28 x 107
Step 3:
Therefore, 0.000000328 converted into standard form is 3.28 × 107.
A standard notation calculator is an alternate way to write numbers in standard form without getting involved into manual calculations.
Daily life applications
The standard form has different applications used in different fields. Here are some common applications of standard form numbers are below,
Scientific and Engineering
Standard form is extensively used in scientific and engineering disciplines to represent extremely large or small numbers. It enables the expression of measurements, distances, masses, and other quantities encountered in scientific and engineering applications in a compact and manageable format.
| Application in | Description |
| Cosmology and Astronomy | The long distances and sizes encountered in science and cosmology often require the use of standard form. It allows scientists to express distances between celestial objects, sizes of galaxies the mass of celestial bodies in a more concise and comprehensible manner. |
| Chemistry and Physics | Standard form finds applications in chemistry and physics when dealing with atomic masses, molecular weights, and energy values. By using scientific notation, scientists can express values such as Avogadro’s number (6.022 × 1023) or the speed of light (2.998 × 108 m/s) in a more manageable and standardized way. |
| Financial and Economic | Standard form is used in finance and economics when representing large numbers associated with budgets, GDP (Gross Domestic Product), national debt, or market capitalization. It simplifies the presentation of these figures and allows for easier comparison and analysis. |
| Computing and Data Storage | In computer science and data storage, the standard form is utilized to express large memory capacities, data transfer rates, or file sizes. It helps in specifying values in a compact format and facilitates data management and communication. |
| Microbiology and Genetics | Standard form is employed in microbiology and genetics to represent the size of organisms, the number of cells or DNA base pairs, or the concentration of chemical solutions. It allows for more efficient and standardized communication of data within these fields. |
Summary
In this article, we have discussed the basic definition of the standard form of numbers, formula, daily life applications, and working standard form of numbers in detail. In addition, the standard form of numbers explains with the help of examples in detail. Everyone understands this article and converts the number into a standard form easily.
FAQs
Question 1:
What is the purpose of using the standard form in numbers?
Solution:
Purpose of the determination of standard form in integers is to represent huge or minor integers in a brief and unchanging arrangement, allowing easier contrast and evaluation of integer crossways with different tips of magnitude.
Question 2:
What is the benefit of expressing small numbers in standard form?
Solution:
The benefit of expressing small numbers in standard form provides simplifying their representation and making them more easily comprehensible. It allows for a concise and standardized format that enables efficient communication and comparisons of values across different orders of magnitude.
Question 3:
How can I convert a large number into standard form?
Solution:
To put a huge number into standard form, shift the decimal point to the left until it is between 1 and 10, and then calculate the number of positions to get the exponent, which will be negative.